Square-1 : méthode de résolution avancée
Ces quelques pages présentent une méthode avancée de résolution du Square-One. Avec un peu d'entrainement, la barre des 30 secondes est atteignable. Il n'y a pas directement de pré-requis à part la notation internationale. En cas d'oubli, son explication est disponible ici.
Toutefois, je pourrais faire référence aux méthodes avancées de 2x2 (ortega/guimond) ou du repérage PLL (fridrich) du 3x3. Même si ce n'est pas quelque chose de nécessaire, cela pourrait aider à la compréhension de connaître ceci.
Cette méthode est très proche de celle que présente Lars Vandenbergh à laquelle j'ai ajouté mes contributions issues de mon expérience. Notez que cette méthode est celle qui est la plus largement utilisée parmis les résolveurs de Square-1 en compétition.
Voici les étapes de la résolution du Square-One que je présente :
Etape 1, retour au cube
Le but de l'étape est d'arriver à obtenir une forme carrée aux deux étages du Square-1 (la tranche du milieu n'a pas besoin de l'être absolument). On appelle souvent cette étape le BTC (back to cube). Cette étape peut descendre à terme facilement en dessous des 5 secondes, toutefois pour un niveau intermédiaire 10 secondes restent acceptables.
Il existe plusieurs méthodes pour ce faire. Une des plus simple est de mettre toutes les arêtes sur la face du haut. Cette manipulation est assez intuitive et elle offre par la suite exactement 5 cas longs pour la plupart pour arriver au cube. La méthode est certes systématique mais comme nous sommes à l'étape de préinspection, il est beaucoup plus efficace de trouver un chemin plus direct dans les 15 secondes qui nous sont alouées.
Préambule
Le BTC est une opération qui nécessite au maximum 7 flips pour être résolus. Il y a 90 cas au total. Bien heureusement, en comprenant correctement une dixaine de cas, il est très facile de s'y ramener en quelques flips ce qui rend cette étape très rapide.
Par mesure de bonne compréhension : les schémas suivant représentent la face du haut et du bas en deux schémas. La face du bas est représentée comme lorsque l'on retourne le cube comme R2 ou x2.
Un premier cas
Afin de donner un premier exemple, voyons le cas qui est reconnu comme un des plus important :
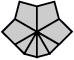
Sa résolution se fait ainsi :
Bien grippé ce BTC se passe en dessous de la seconde. Remarquez que chaque position intermédiaire à la résolution du BTC est en soit un cas à connaître.
Réduction au cas
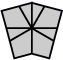
Voyons désormais comment résoudre la position:

Il est possible de revenir dans la situation précédente en deux flips seulement.
Détaillons pourquoi et comment ça marche.
- Dans le premier cas, on décide de garder les deux arêtes attachés ensemble. Les deux en angle droit vont se coller au bloc de 4. De ce fait, on a directement la formation de deux arêtes opposés. On a donc un bloc de 2, un de 4 et deux arêtes opposés. On peut former le BTC que l'on désire.
- Dans le deuxième cas, on décide de faire l'inverse en transformant les deux arêtes opposés en deux arêtes en angle droit. Nous obtenons donc un bloc de 4, et deux blocs en angle droit.
En général
Il vous faut vous baser sur les quelques BTC connus et rapides. Par la suite, il faut trouver une (ou des) réduction(s) rapide(s). Une fois la réduction calculée, tout doit aller très vite et pourrait se faire à l'aveugle. Le but final étant d'avoir un nombre très restreint (voire nul) de cas sur lequel vous n'avez pas de stratégie rapide.
De plus, il est très conseillé de savoir comment passer le même BTC en mirroir derrière (pour éviter de faire (6,6) dans le vide) et avec les étages inversés.
Le but de l'étape est d'avoir les coins des deux faces du Square-1 rassemblés. Pour ceux qui connaissent la méthode Guimond, cette étape est très très intuitive et peut être résolue en 3 flips maximum.
La méthode
- Si vous connaissez les séquences de séparation de Guimond, il vous suffit de commencer par un (1,0) afin toujours conserver votre forme cubique. À partir de là, si on remplace U par (3,0) et R2 par /, les séquences sont exactement les mêmes.
- Pour les autres, le principe est très simple mais à but informatif et aussi de rapidité d'exécution, voici l'ensemble des séquences.
Remarquez la présence du (1,0) qui ne fait que conserver l'état cubique du Square-1.
Expert : Anticiper l'étape d'après
C'est un fait acquis, l'anticipation est la clef de la vitesse. Ici, en plus de pouvoir anticiper la prochaine étape sur la séparation des arêtes lors du dernier flip notamment, il est aussi possible de "forcer" le skip. En effet, au lieu d'avoir un (1,0)/.../(-1,0), il peut être intéressant de faire (0,-1)/.../(0,1). Le principe reste le même pour les coins mais les blocs de coins/arêtes ne seront pas les mêmes. Dans les cas simple, il est possible avec un peu d'expérience de pouvoir forcer un skip de la prochaine étape. L'idée pour forcer le skip est de séparer le moins possible les arêtes des coins lorsqu'ils sont de la même couleur.
Attention toutefois, cette optimisation ne s'applique qu'aux cas simples et dans la plupart des résolutions ceci ne sera pas possible directement. Il ne faut pas perdre du temps à analyser si on ne trouve pas d'un coup d'?il qu'une stratégie est préférable à l'autre.
Le but de l'étape est d'avoir les arêtes des deux faces du Square-1 rassemblés. Ici, il devient dur d'appliquer les connaissances des autres cubes dans le sens ou il faut jouer sur le principe du (1,0), inexistant ailleurs.
La méthode
Le principe reste le même, on reconnait un cas et on l'applique. Toutefois, il existe trois classes de cas principaux.
-
Le cas très simple (et son dérivé)
Je conseillerais aux débutants de bien travailler le premier cas. Sa manipulation est très simple et à faire en aller-retour direct. Entendez par là qu'il n'y aura absolument aucun regrip. Le deuxième cas, quant à lui n'est que le premier fait deux fois avec un (3,3) entre temps. Ces cas conservent les positions de coins.
-
Les cas indispensables
Ces cas sont ceux qui reviennent directement même dès le début. Il faut absolument savoir les passer rapidement.
-
Les cas plus difficiles.
-
Ces cas ne sont pas extrêmement difficiles en vérité, mais ils ne sont pas absolument indispensable. En effet, il suffit de faire (1,0)/(-1,1)/(1,0), ou de faire attention lors de la précédente étape, pour revenir aux précédents cas.
Le dernier cas inverse le haut et le bas en plus. Si vous voulez garder le contrôle, vous pouvez changer le (3,0)/(-1,0) par (-3,6)/(0,1) qui est plus difficile à passer.
Expert : Anticiper l'étape suivante
L'étape suivante étant le placement de coins. Il sera certes facile de repérer cette étape mais il est parfois nécessaire de regarder sur la face de derrière. Il peut être intéressant d'avoir plusieurs informations avant de finir cette étape. Dans la liste ci-dessous, vous trouverez les influences des séquences présentés dans cette page. Par ordre d'apparition :
- Conserve tout
- Conserve tout
- N en haut, et J en bas (coins conservés DFL, DBL)
- Conserve tout
- Double J (barres UF et DR)
- Double J (barres UR et DB)
- Double J (barres UB et DL)
En utilisant les cas qui conservent tout et des principes de setup, il est toujours possible de résoudre sans rien casser.
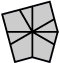
En l'état, vous devez avoir un puzzle sous forme cubique (sans compter la tranche du milieu), sur chacune des deux faces vous devez avoir un square-1 dans un état similaire à ça :
Comme le nombre de cas pour achever le tout est encore très grand, nous allons résoudre les coins. Pour ceux qui connaissent la méthode Guimond ou Ortega en 2x2, ils ne seront pas dépaysés. En effet, les séquences présentes dans cette pages sont aussi applicable pour la dernière partie d'une résolution de 2x2. Seulement, la différence réside dans le fait que le mouvement F2 est interdit, tout comme R. Voyons la liste complète :
Les séquences
Toutes ces séquences appliquent des PLL J ou des PLL N sur chacune des faces. Vous remarquerez la simplicité des cas qui ne sont composés que de (3,0) et similaires.
-
Les cas qui n'appliquent des changements que sur une face
-
Les cas qui s'appliquent sur les deux faces (eux très similaires à Ortega)
Expert : Forcer le skip
Encore une fois, on peut forcer le destin pour la prochaine étape. Comme précisé précédemment, ces séquences ne produisent que des PLL N ou J ou conservation totale. Dans les premiers cas, un étage sera conservé donc on peut déjà avoir repérer quelques informations, comme le nombre d'arêtes positionnés ou s'il y a parité, voire la forme complète si on y arrive.
Mais on peut aussi agir sur les comportements des séquences présentes ici. Supposons que l'on tombe sur ce cube :
On a effectivement deux J pures. Le problème étant que si l'on attaque directement avec la formule présentée, on va se retrouver avec un PLL U en haut (application de J au lieu de Jsym et inversement). Pour remédier à ça, on peut faire (1,0), la séquence, et (-1,0). Le premier mouvement va permettre au bloc coin-arête de ne pas se faire couper. On aura donc résolu le cube en un seul coup !
Une règle majeure restera donc d'essayer de ne pas couper les blocs coins-arêtes par de petits ajustements tels que (1,0), (0,-1) ou (1,-1)
Si vous savez utiliser correctement Fridrich sur un 3x3, vous pouvez aussi repérer les PLL qui sont formés. Si la PLL existe, alors il n'y aura pas parité sur cet étage. Notez que si les deux étages ont une parité, elles se compenseront.
Expert : Corriger la parité
Comme on l'a vu dans la section précédente. Il est possible d'anticiper sur le fait qu'il y ai parité ou non. Si effectivement, il y a parité sur un seul des deux étages, alors il est possible d'appliquer une séquence qui corrige la parité en permuttant les coins. La liste des séquences est disponible ci-dessous.
Évidemment, cela a une contrepartie, comparé à la méthode classique. Il devient impossible de contrôler le skip pour la suite, ou le nombre d'arêtes à placer. Par contre, le nombre de cas est plus restreint pour la suite et bien plus rapide en général. Le choix de la méthode à utiliser vous appartient.
Etape 5, Placement des arêtes
Cette étape est une de celle qui prend le plus de temps et qui serait assimilable au dernier étage du 3x3. Le principe reste simple si on veut apprendre la liste complète des permutations. Le problème étant qu'il y en a beaucoup au total (une centaine en fait, symétries haut/bas comprises).
Je montrerai ici comment augmenter son ensemble de séquences progressivement en ayant au fur et à mesure le moins de choses à faire. La liste complète des cas peut se trouver ici CubeZone: Square-1 EP
En tant que préambule, je rappelle que le square-1 est un cube à parité, car il change de forme et le cube peut ne pas être entièrement résolvable en conservant la forme cubique. Ces cas-là peuvent se repérer si vous êtes notamment au courant des EPLL de Fridrich 3x3 par exemple. Si un seul des étages a une EPLL inconnue, alors il y a parité. Ces cas-là sont un peu plus longs à exécuter la plupart du temps.
Le kit vraiment minimal
Résoudre la fin d'un square-1, c'est soit faire preuve de patience et apprendre l'ensemble des cas, soit se contenter de peu et utiliser un peu de ruse. Le kit minimal pour savoir résoudre efficacement un square-1 se décompose en deux séquences principales ainsi qu'une parité.
Quelques commentaires sur ceci. Tout d'abord, si vous n'avez pas de parité. Tout le cube peut se résoudre facilement avec les deux premières séquences. Leur exécution est extrêmement rapide et elles se comprennent bien en voyant que les mouvements tels que /(1,1)/ sont des M2. Ainsi, la première séquence pourrait se traduire sur un 3x3 par M2 U2 M2 U2. Et la deuxième par U' R2 D M2 D' R2 U
Le double adjascent peut se passer par derrière aussi : (-2,0)/(3,0)/(-1,-1)/(-2,1)/(2,0). Ceci évite de faire des réalignements vraiment contraignants tels que (6,6) qui n'est pas très sympathique à passer.
Mon choix de parité n'a pas été facile, car plusieurs parités existent et ce n'est pas la plus courte. Par contre, elle peut passer de façon très rapide même sous stress, car les mouvements sont très automatiques. Les seuls mouvements possibles à chaque fois sont souvent les bons ce qui évite des erreurs. De plus, il respecte bien l'enchainement des mouvements de la main.
Vous accorderez une grande attention à la résolution de la parité. Suivant où vous l'appliquerez, ses implications ne seront pas les mêmes. Quitte à faire une parité autant vous épargner du boulot, non ?
Les combinaisons classiques avec le kit minimal
Voici ci dessous, une liste non exhaustive de combinaisons que l'on peut faire avec ce petit kit.
-
Double U (i.e. double trois-cycles) : Double Opposés, puis Double Adjacent. Notez que le principe est le même pour toutes les sortes de 3-cycles. Il vous suffit de mettre les barres à droite ou à gauche.
-
Double Z : Double Adjacent deux fois (de plus des mouvements s'annulent en faisant le deuxième par derrière)
Double H : Double Opposés deux fois avec un (3,-3) inséré entre les deux
- PLL H : Double Opposés deux fois avec un (3,0) inséré entre les deux
- PLL Z / U : Double adjacent sera de mise. Il faut toujours commencer son premier par une paire de la Z avec une partie de la U qui a la couleur opposé.
Le kit suffisant
Ce kit de cas, vous permettra de résoudre la plupart des cas de façon très rapide. Notez que le kit minimal permet de les résoudre mais vous constaterez leur importance.
-
PLL U (3-cycle) : Même si sa taille semble longue, son exécution est très rapide ce qui en fait une séquence absolument importante. Vous trouverez les différents inverses-symétries si besoin.
- PLL Z : Cette séquence est basée sur M2 puisque son principe est M2 U M2 U' M2. Sur un 3x3, elle n'est pas applicable car il y a un nombre impair de M2, ici ce n'est pas grave. Notez que les séquences basées sur M2 ont l'avantage de se symétriser Haut/Bas de façon naturelle.
- Rond / Opposé : En faisant une légère variante de la Z, on obtient celle-ci par M2 U M2 U M2. Notez que vous pouvez partir à gauche (U) comme à droite (U') suivant le sens du rond (répérez l'emplacement cible de l'arête en UF).
- PLL H : Encore une M2. Si vous connaissez celle du 3x3, c'est la même M2 U M2 U2 M2 U M2
- Adjacent / Opposé : Voilà un premier exemple de séquence difficile mais qui reste indispensable car les solutions de remplacements restent longues (Double Opposés et PLL U).
- Parité Rond : C'est la parité la plus simple à comprendre. Le principe étant de former une étoile de 6 coins sur U. On applique ensuite un 6-cycle en faisant (2,0) ou (-2,0) introduisant la parité, et on refait le BTC avec le rétablissement du cube en 2 flips supplémentaires. Si le rond est horaire il faudra appliquer (-2,0) et inversement. Pour la rapidité, je vous conseille de voir de quel côté se trouve l'arête qui correpond aux coins sur UF.
- Parité U / Adjacent : Elle n'a pas belle allure, mais elle se rencontre vraiment souvent, surtout lorsque l'on contrôle l'étape précédente. Il est important de connaitre l'ensemble des inverses-symétries sur un tel cas, pour plus de simplicité elles sont à disposition ici. Avec de l'entrainement, elles passeront plus rapidement que Double Adj-Parité Adj.
Et le reste ?
Si vous connaissez déjà toutes les permutations ici présentes, vous êtes à un niveau bien avancé. Je vous conseille de bien vous entrainer à faire ces quelques EP et de trouver leurs symétries si besoin. Enfin, si vous avez besoin d'autres EP, vous pouvez vous tourner vers la liste complète que vous pouvez trouver sur le site de Lars Vandenbergh
Quelques astuces supplémentaires
Avec juste ces quelques EP, vous avez tout pour tomber en dessous des 25 secondes de moyenne. Vous aurez remarqué que beaucoup de ces séquences sont simples au final et bénéficient d'une vitesse d'exécution très impressionnante. Il n'est pas toujours utile d'aller chercher la séquence optimale de résolution d'un cas complexe car une combinaison efficace de deux des cas précédents vous permettra, la plupart du temps, une réussite rapide. Quelques cas isolés sont plus délicats, notez que vous pouvez les enlever avec M2 U2 M2
Ne doutez pas de la puissance de l'alignement dans l'étape d'avant. En effet, si vous avez au moins un bloc coin-arête (cas fréquent). Sauver ce bloc restreindra la liste des possibilité d'EPLL sur cet étage à : Adjascent, Opposé, U et U'. Donc, on enlève tous les cas difficiles et on garde que des cas rapides. Avec un peu d'expérience, il est possible de compter le nombre d'arête à permuter avant l'exécution de l'étape d'avant.
Soyez astucieux lors du placement de votre parité. Quand vous ne connaissez que peu de parités, l'endroit où vous allez l'exécuter change drastiquement les configurations. Admettons que vous ayez Adj/Z. Admettons que vous appliquiez la parité adjacente pure. Un mauvais alignement de départ vous donnera U/Z, sympathique certes, mais dommage. Un bon alignement vous donnera Skip/Z. Vous pouvez vous contenter du double Z, un peu plus long mais très efficace.
Il est extrêmement important de savoir comment se comporte la tranche du milieu par rapport aux séquences que vous exécuterez. Vous saurez ainsi directement avant la fin de votre résolution de l'étape ce qu'il faudra faire pour la suite. Dans les différents kits précédents, seules : la parité adjacente, le cas Adjacent/Opposé et son symétrique inversent la position de la tranche centrale. Une astuce pour gagner un peu de temps est d'intégrer la dernière étape aux séquences que vous exécutez. Avec l'expérience, vous arriverez à la faire naturellement sans passer par l'état stable, arrivant ainsi directement à la fin.
Etape 6, Correction finale
Ça y est vous êtes bientôt au bout de vos peines. Il ne reste que trois séquences ultra-simplistes pour achever votre Square-1. Il vous faut corriger, si besoin, la tranche centrale, ainsi que la position des deux étages désormais. En dehors de l'état résolu, il n'y a que trois cas.
| Echange haut-bas : /(6,6)/(5,-5) | Tranche centrale : /(6,0)/(6,0)/(6,0) | Les deux : /(6,0)/(0,6)/(5,1) |
Notez que pour plus de rapidité sur la fin, il est conseillé de prévoir cette étape pendant la résolution de l'étape précédente.
Et voilà, vous savez résoudre un Square-1. Félicitations !
