Résoudre le Rubik's cube sans regarder, ou blindfold
On va présenter ici la méthode 3-cycles.
On va pour ceci totalement changer de méthode sinon c'est impossible :P . On va donc utiliser le méthode des cycles. Celle-ci se déroule en quatre temps. Je vais ajouter aussi en commentaires le façon dont je mémorise les étapes à faire. Le blindfold cubing demande cependant de bien connaître certaines chose.
La première chose à savoir est qu'on va numéroter chaque coin et lettrer chaque arête. Voici la façon dont je m'y prend :
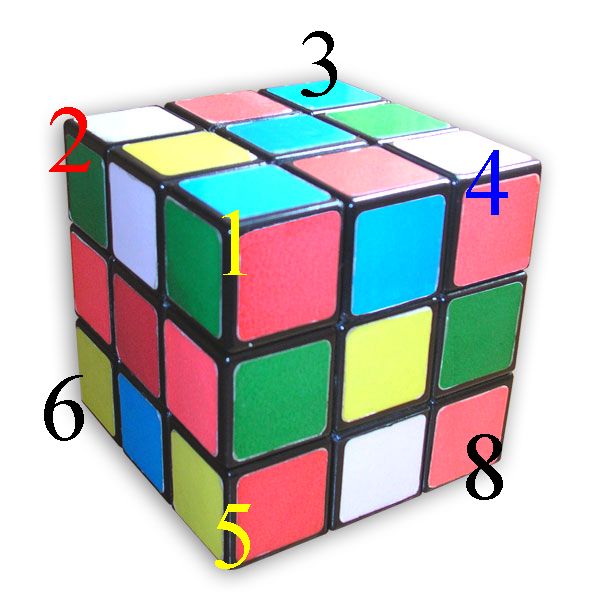
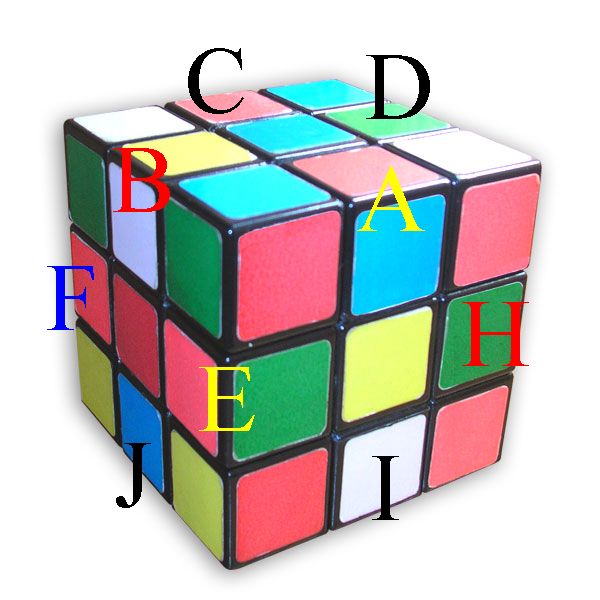
Pour résoudre le Rubik's cube les yeux bandés avec la méthode des cycles, les étapes sont les suivantes :
Étape 1 : Orienter les coins
Ca pourrait paraître facile, mais afin de ne pas modifier le reste du cube et ne faire qu'orienter les coins, il va falloir utiliser des passes dites conservatives, c'est a dire qu'elles ne font que retourner les coins et rien d'autres. Chaque coin a trois orientations. Il faut donc pour bien l'orienter le tourner ou dans un sens, ou dans l'autre, voir le laisser tel quel. Ces deux sens seront le sens des aiguilles d'un montre (cw : clockwise) ou le sens contraire (ccw : counterclockwise). Je mémorise les coins à tourner par deux ou trois de la facon suivante : dans chaque groupe de deux, le premier est cw et le second ccw. Dans les groupes de trois ils sont tous à tourner dans le même sens, il faut donc aussi retenir le sens. On a ici par exemple a retenir (13)(247 cw). Ce qui est complètement faisable ;). D'autre personnes, ayant une mémoire visuelle, préfèrent mémoriser la position des stickers jaunes et blancs des coins.
C'est bien beau de savoir comment retourner les coins, mais voilà : lesquels retourner ? La règle est simple : chaque coin doit avoir sa couleur U/D sur la face U/D. Moi qui mets toujours le jaune en haut, je dois avoir les stickers jaunes et blanche des coins sur les faces jaunes et blanches du cube.
Nous presentons de nombreux cas ici, il suffit en réalité d'en connaître un seul. Bien sur, on peut aller plus vite en en connaissant plus.
Voici comment vous en sortir sans rien modifier d'autre :
Si vous n'êtes dans aucun de ces cas, il vous est possible d'utiliser une astuce : chercher dans votre tête une transformation du cube qui vous met dans un des ces cas. Nous allons l'appeler P et la mémoriser. On résout le cas dans lequel on se retrouve grâce à P. Ensuite on applique P-1 , c'est a dire l'inverse de P.
Voir ici pour inverser une passe
Étape 2 : Orienter les arêtes
Ici, c'est plus simple etant donné que les arêtes n'ont que deux sens possibles. Elles sont ou bien orientées ou mal orientées. On ne retient donc que quelque chose du genre ABDFJK. Facile aussi non ?
Par contre, savoir si elles sont bien orientées ou non est plus difficile. Les règles sont simples :
- Une arête avec une couleur U/D sur une face U/D est bien orientée.
- Une arête avec une couleur L/R sur une face L/R est bien orientée.
- Une arête avec une couleur U/D sur une face L/R est mal orientée.
- Une arête avec une couleur L/R sur une face U/D est mal orientée.
Dit comme ca ca peut paraître très compliqué. Il faut en fait que l'arrete puisse aller a son emplacement, et dans le bon sens, en utilisant simplement les faces L,R,U et D Voici la manière visuelle de le dire, qui à mon avis est beaucoup plus simple.
Position des couleurs U/D
Position des couleurs L/R
Bon mais voilà, comment on retourne ces arêtes ? Et bien on va se referer aux cas suivants :
Il est bien sûr possible et conseillé d'utiliser P ici aussi.
Étape 3 : Placer les arêtes
Nous allons utiliser ici la méthode des cycles. Nous allons définir des cycles et les résoudre sur le cube. Ne fuyez pas déjà, ca n'est pas si dur qu'il y paraît et avec un peu de travail on y arrive. Comment définit-on un cycle ? Il suffit pour cela de choisir une arête A par exemple. On regarde où doit aller se positionner cette arête -disons en D. On observe ensuite l'arête en D et on se pose la même question. Arrive un moment où l'on retombe en A, et on a fait un cycle. Toutes les arêtes mal placées doivent faire partie d'un cycle, il est donc possible d'avoir plusieurs cycles sur le même cube. On va mémoriser un cycle par une suite de lettres par exemple, ADFIJ signifie que l'arête positionnée en A doit aller en D, l'arête positionnée en D doit aller en F et ainsi de suite. L'arête positionnée en J doit aller en A. Un exemple typique de ce que vous aurez à mémoriser est : (ADFIJ)(BCKGLE).
Continuons l'exemple (ADFIJ)(BCKGLE). Nous allons d'abord réaliser ADF. La pièce qui était en A va aller en D, celle en D va aller en F et celle en F va aller en A. On aura donc les pièces en D et en F bien placées. La pièce en A sera celle anciennement en F et devra donc aller en I. Ainsi, on aura réduit nos cycles à (AIJ)(BCKGLE). On va donc toujours résoudre les pièces trois par trois et enlever les deux dernières du cycle. Cela est très pratique au niveau mémorisation, car on peut oublier ce qu'on a déjà fait et se concentrer sur la suite.
Ainsi, on résout d'abord les cycles de longueur supérieure ou égale à 3 :
Faces : U/D et L/R
Faces : F/B
Les cycles de longueur 2 se résolvent 2 par 2, grâces aux passes suivantes, et après avoir résolu les cycles plus longs :
Faces : U/D et L/R
Faces : Toutes
Pour résoudre les cycles, nous allons encore nous baser sur la passe P. A ceci près que nous ne pouvons pas faire n'importe quoi ! En effet, il ne faut pas désorienter les arêtes. pour ceci, nous allons interdire les mouvement F, F', B, B'. Rassurez vous, il est tout a fait possible de s'en sortir comme ça.
Étape 4 : Placer les coins et parités
Ici, nous allons aussi utiliser la méthode des cycles. Seules les passes changent. Nous retenons quelque chose du genre (156)(2438), ce qui a la même signification que dans l'étape précédente. Beaucoup de gens considèrent que cette étape est plus facile que celle consistant à replacer les arêtes. Personnellement, je la trouve plus difficile, car les limitation sur P obligent parfois à une gymnastique mentale des plus périlleuses . . .
Faces : U/D
Il va falloir ensuite résoudre ces cycles. Pour ceci nous allons n'utiliser qu'une passe pour les cycles de longueur supérieur ou égale a 3 (et ses miroir et/ou inverse). Bien sur, cela nous oblige à utiliser P. De plus, nous avons orienté les coins, pour ne pas les désorienter, nous allons interdire les mouvements L, L', R, R', F, F' B, B' dans P. Les mouvements des tranches de milieux sont interdits (et inutiles) !! Il est par contre possible de tourner le cube dans tous les sens, à condition de laisser une des faces U/D en haut.
Continuons l'exemple (156)(2438). De même que précédemment, on résout 156 qui finit le premier cycle, puis 243 qui réduit le deuxième cycle a 28.
Les cycles de longueurs 2 se résolvent 2 par 2, grâce aux passes suivantes :
Faces : Toutes
Faces : U/D
Astuces pour les cycles de longueur supérieure ou égale a 3: Ici, P peut parfois devenir difficile, notamment dans les cas de cycles de longueur 3 dont les pièces sont sur plusieurs faces. Voici quelques exemples qui sans doute vous aideront.
Ici, on a un cycle sur la face R, la pièce étant destinée a la face D est a la verticale de sa position.
Ici, on a un cycle sur la face L, la pièce étant destinée à la face D n'est pas à la verticale de sa position.
Ici, on a un cycle "diagonal" sur le cube. Un cas pas évident sans cette astuce. On peut facilement transformer le cycle inverse en utilisant P = U2.
Astuces pour les cycles de longueur 2 : Ici aussi, on va utiliser des combinaisons des passes précédentes pour se simplifier la tâche.
Conversion d'un cycle de longueur 2 en diagonal en cycle de longueur 2 non diagonal. Cette conversion est très utile pour résoudre les problèmes de parité.
On ne s'occupe pas des arêtes ici.
Cas où la passe P ne respecte pas les règles mais qui marche. cela est parfois possible avec les cycles de longueur 2. Se produit quand des coins échangés sont désorientés de la même façon.
Cas semblable au précédent. Ce genre de pratique n'est à utiliser que sur des cas que l'on connaît.
Vous croyez vous être sorti(e) d'affaire ? Et bien détrompez vous, car sauf si vous avez de la chance (selon les probabilités, c'est 50%), vous aurez un problème de parité, c'est a dire qu'il vous restera a résoudre une paire d'arête et une paire de coins. Comment faire ? Tout d'abord, il va falloir utiliser P. Mais ici le problèmes est que P peut devenir long. Afin de se faciliter la tâche, On va tourner les faces pour mettre les deux coins là où l'on veut, en respectant les mêmes limitations que pour les coins, et placer les arêtes avec des mouvements des tranches du milieux plus ceux des faces U et D. Attention, vous ne pouvez utiliser que M2, S2, E2, U, U2, U', D, D2, D' pour placer les arêtes. Il est possible d'utiliser en plus les faces ou il n'y a pas les coins. Il va enfin falloir utiliser une des passes suivantes et effectuer P-1 .
On va ensuite utiliser les passes suivantes :
Faces : U/D
Faces : U/D et L/R
Faces : toutes
Enfin, s'il n'y a pas de passe P simple, plutôt que de faire une erreur (ca serait bête rendu a ce stade :P), il vaut mieux résoudre une des paires de coins grâce à une des passes ci-dessus. On a ensuite des paires d'arêtes a résoudre, il faut donc reprendre l'étape 3 et on a finit le cube ;).
