Les mathématiques du rubik's cube
Sommaire
Dénombrement
Calcul du nombre de combinaisons possibles pour un rubik's cube
Le rubik's cube est composé de 12 arêtes et 8 coins et de 6 centres. On va prendre les centres comme point de repère, de plus une rotation sur lui-même d'un centre n'a aucune conséquence sur le cube, on ne va donc pas les considérer.
- Les 12 arêtes peuvent chacune s'orienter dans deux directions. La direction de la dernière arête est fixée par la direction des arêtes précédentes, cela nous donne donc 211possibilités d'orientations des arêtes.
- Les 8 coins peuvent chacun s'orienter dans trois directions. La direction du dernier coin est fixée par la direction des coins précédents, cela nous donne donc 37possibilités d'orientations des coins.
- Les 12 arêtes peuvent se répartir dans 12 emplacements. Cela nous donne donc 12! possibilités de placement des arêtes.
- Les 8 coins peuvent se répartir dans 8 emplacements. Cela nous donne donc 8! possibilités de placement des coins. Mais il n'est pas possible d'échanger 2 coins ou deux arêtes seulement (mais il est possible d'échanger deux coins ET deux arêtes seulement), les derniers deux coins n'ont donc pas deux solutions pour se placer mais une seule et le résultat est divisé par deux. On va répercuter cette division par deux dans le 211qui va devenir 210.
On arrive donc a un total de 12!*8!*37*210= 479 001 600 * 40 320 * 2 187 * 1 024 = 43 252 003 274 489 856 000
Pour info, la décomposition en facteurs premier donne : 227*314*53*72*11 = 134 217 728 * 4 782 969 * 125 * 49 * 11 = 43 252 003 274 489 856 000
En français, ce nombre est : quarante-trois milliards deux-cent cinquante-deux millions trois-mille deux-cent soixante-quatorze de milliards quatre-cent quatre-vingts-neuf millions huit-cent cinquante-six mille.
Certains rubik's cubes ont des dessins sur les faces. L'orientation des centres devient alors importante et il faut multiplier le résultat précédent par 2*45= 211= 2 048 car l'orientation du dernier centre est fixée par celle des autres centres au demi-tour près. On arrive donc à 12!*221*8!*37= 479 001 600 * 2 097 152 * 40 320 * 2 187 = 88 580 102 706 155 225 088 000
Calcul du nombre d'algorithmes en n coups
Le rubik's cube possède 6 faces qui peuvent être tournées dans un sens, dans l'autre, et faire des demis tours. Cela nous fait donc 6*3 = 18 coups existants. Mais lorsqu'on a tourné une face, on n'aboutit à rien si on tourne à nouveau cette face. Il faut donc qu'après le premier coup, on se limite à 18-3 = 15 possibilités de rotations. Le nombre d'algorithmes en n coups est donc de 18*15n-1. Autant dire que l'arrivée des ordinateurs dans le monde du rubik's cube a permis une très nette avancée dans la découverte des algorithmes intéressants. Il est aussi à noter que beaucoup de ces algorithmes peuvent revenir au même, notamment les algorithmes de période 2 et leur inverse et tous les algorithmes dans lesquels ils sont inclus et les algorithmes équivalents. Ce calcul n'a donc aucun lien avec le nombre de positions différentes que vous atteindrez en n coups, mais le nombre de façons différentes que vous aurez à votre disposition pour les atteindre.
Notions mathématiques sur les algorithmes
Périodicité des algorithmes
TOUS les algorithmes quels qu'ils soient sont périodiques. La période d'un algorithme est le nombre de fois que vous devez faire cet algorithme pour revenir à votre position de départ. La période d'un algorithme ne dépend que de l'algorithme.
La notion de périodicité va prendre tout sont intérêt combinée avec la notion d'inversibilité. Le fait que tous les algorithmes soient périodiques vient du fait que le rubik's cube a un nombre fini de possibilités (voir partie dénombrement).
Exemple d'algorithme de période 2. On voit bien que quand cet algorithme est appliqué deux fois, on revient à la position de départ.
Inversion des algorithmes
Ici aussi, tous les algorithmes sont inversibles. Un algorithme est l'inverse d'un autre, si quand on effectue les deux à la suite, on retombe sur sa position de départ. On peut donc noter que les algorithmes de période deux sont inverses d'eux-mêmes, mais ceci est un cas particulier.
Tous d'abord, avant ces explications, mettons-nous d'accord sur les notations. si a est un algorithme, a' est son inverse. Si a et b sont deux algorithmes, on note ab le fait de faire ces deux algorithmes à la suite. On peut écrire les propriétés suivantes :
- a'' = a, a est donc l'inverse de a'.
- L'inversion des mouvements de base est la suivante : (L)' = L' (d’où la notation), L''=L (voir propriété 1) et L2' = L2 (voir dernière 6, L2 est de période 2).
- ab diffère de ba. Prenons comme exemple a = R et b = F pour faire simple. RF diffère de FR. Ceci revient à dire que l'ordre dans lequel vous tournez les faces a de l'importance.
- (ab)' = b'a', ceci revient à dire que si vous avez fait RF, il vous faudra faire F'R' pour revenir à votre point de départ.
- On déduit des deux précédentes que (ab)' est différent de a'b'
- Si a est de période n, an-1= a'
Pratiquons un peu car ces considérations mathématiques doivent vous paraître abstraites. Prenons par exemple l'algorithme a = R2U2R2U2. Cet algorithme est de période 3. On a donc a2= R2U2R2U2R2U2R2U2 = a'. Mais, en inversant cet algorithme avec la propriété 4, on obtient a' = U2R2U2R2, qui aura le même effet que R2U2R2U2R2U2R2U2, mais sera bien plus vite exécutée.
Cette propriété est très utilisée en speedcubing, notamment avec certaines PLL.
Algorithmes miroirs ou symétriques
Le rubik's cube, comme son nom l'indique, est un cube, et a donc de nombreux axes de symétrie. Trois symétries vont nous intéresser ici. D'autres existent, mais ne sont pas intéressantes humainement parlant De plus, la méthode sera la même pour ces symétries, donc si vous vous y intéressez ce document devrait être suffisant.
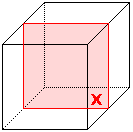
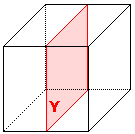
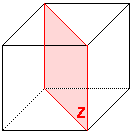
De plus, on peut noter que la symétrie X peut facilement se convertir en symétrie Y de la façons suivante :

La position de base.

La position miroir selon X.

Revient à la position miroir selon Y si l'on fait un demi-tour de 180°.
Les algorithmes symétriques ont deux utilités. Si la position est déjà symétrique, faire l'algorithme symétrique revient au même résultat. Cela sert en speedcubing à exécuter les algorithmes des cas symétriques avec la main la plus rapide. Une deuxième utilité est de pouvoir résoudre deux cas symétriques en n'apprenant qu'un seul algorithme.
Tout ça c'est bien beau, mais comment crée-t-on un algorithme miroir ? Les néophytes pourront se référer au tableau ci-dessous, mais très vite, cela vous semblera intuitif (normalement).
| Faces | U | U' | U2 | R | R' | R2 | L | L' | L2 | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symétries | X | U' | U | U2 | R' | R | R2 | L' | L | L2 | ||||||||||||||||
| Y | U' | U | U2 | L' | L | L2 | R' | R | R2 | |||||||||||||||||
| Z | U' | U | U2 | F' | F | F2 | B' | B | B2 | |||||||||||||||||
| Faces | F | F' | F2 | B | B' | B2 | D | D' | D2 | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symétries | X | B' | B | B2 | F' | F | F2 | D' | D | D2 | ||||||||||||||||
| Y | F' | F | F2 | B' | B | B2 | D' | D | D2 | |||||||||||||||||
| Z | R' | R | R2 | L' | L | L2 | D' | D | D2 | |||||||||||||||||
Comment ce tableau est-il rempli ? Ça n'est pas compliqué, il y a deux règles pour trouver la face qu'on va tourner et dans quel sens. Concernant le sens, c'est très facile : c'est toujours dans le sens inverse au sens d'origine. Concernant la face à tourner, c'est un peu plus délicat, c'est la face qu'on obtient par symétrie par rapport à l'axe choisis, mais je vous conseille de regarder comment ça se passe sur votre cube, c'est beaucoup plus simple à comprendre qu'une tartine de texte.
À gauche, deux algorithmes symétriques selon Z. La situation est symétrique, on va donc choisir l'un ou l'autre en fonction de la rapidité avec laquelle on va l'exécuter. Ceci n'a d'intérêt qu'en speedcubing.
À droite, deux algorithmes symétriques selon Y. Ils permettent de résoudre deux cas symétriques. Savoir faire le miroir d'un algorithme permet de ne pas avoir à en apprendre trop.
NB : Dans la méthode de Fridrich ou de Petrus, les réflexions selon Z servent lors de la résolution des deux premières couronnes, alors que les réflexions selon X et Y servent à faire la dernière face.
NB : Le cas d'une symétrie par rapport à une droite n'est pas traité ici, mais il est déductible : une symétrie par rapport à une droite est en fait une symétrie par rapport à un plan, puis par rapport à un autre. Enfin, la symétrie par rapport à un point est une symétrie par rapport à une droite et par rapport à un plan dans lequel la droite n'est pas contenue.
Conservativité des algorithmes.
Ça y est, on sort les mots barbares. En fait ça n'est pas très compliqué. La conservativité d'un algorithme est ce qu'il ne va pas changer dans le cube. On va donc chercher à n'utiliser que des algorithmes conservatifs de ce qu'on a déjà construit dans le cube quand on va le résoudre. Par exemple, tous les algorithmes utilisée lors de la dernière étape de la méthode Fridrich sont conservatifs de l'orientation des cubes, mais non de leur position.
En général, plus un algorithme est conservatif, plus il est long. C'est pourquoi on va utiliser des algorithmes qui ne sont conservatifs que de ce qu'on a déjà construit dans le cube. En blindfold, le problème est différent. Comme on ne peut pas regarder le cube entre chaque étapes de la résolution, on se doit d'utiliser des algorithmes qui sont conservatifs de tout, sauf de ce qu'on veut leur faire faire en particulier.
Les deux algorithmes ci-contre ont le même effet sur l'orientation des coins. L'un est conservatif de la position, l'autre non. L'algorithme conservateur est utilisé en blindfold, il existe d'autres algorithmes qui ont le même effet et qui sont conservateurs en moins de mouvement, mais ils sont plus difficiles à exécuter les yeux fermés.
